4468: B. Prefix Sum Addicts

Suppose a₁, a₂, ..., a_n is a sorted integer sequence of length n such that a₁ <= a₂ <= ... <= a_n.
For every 1 <= i <= n, the prefix sum s_i of the first i terms a₁, a₂, ..., a_i is defined by

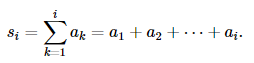
Now you are given the last k terms of the prefix sums, which are s_n-k+1, ..., s_n-1, s_n. Your task is to determine whether this is possible.
Formally, given k integers s_n-k+1, ..., s_n-1, s_n, the task is to check whether there is a sequence a₁, a₂, ..., a_n such that

1. a₁ ≤ a₂ ≤⋯≤ a_n, and
2. s_i = a₁+ a₂+⋯+a_i for all n−k+1 ≤ i ≤ n.

Each test contains multiple test cases. The first line contains an integer t (1 <= t <= 10⁵) — the number of test cases. The following lines contain the description of each test case.
The first line of each test case contains two integers n (1 <= n <= 10⁵) and k (1 <= k <= n), indicating the length of the sequence a and the number of terms of prefix sums, respectively.
The second line of each test case contains k integers s_n-k+1, ..., s_n-1, s_n (-10⁹ <= s_i <= 10⁹ for every n-k+1 <= i <= n).
It is guaranteed that the sum of n over all test cases does not exceed 10⁵.

For each test case, output "Yes" or "No". 

4
5 5
1 2 3 4 5
7 4
-6 -5 -3 0
3 3
2 3 4
3 2
3 4

Yes
Yes
No
No

In the first test case, we have the only sequence a = [1, 1, 1, 1, 1].
In the second test case, we can choose, for example, a = [-3, -2, -1, 0, 1, 2, 3].
In the third test case, the prefix sums define the only sequence a = [2, 1, 1], but it is not sorted.
In the fourth test case, it can be shown that there is no sequence with the given prefix sums.