4465: B. Tea with Tangerines
题目描述
There are n pieces of tangerine peel, the i-th of them has size ai. In one step it is possible to divide one piece of size x into two pieces of positive integer sizes y and z so that y+z=x.
You want that for each pair of pieces, their sizes differ strictly less than twice. In other words, there should not be two pieces of size x and y, such that 2x ≤ y. What is the minimum possible number of steps needed to satisfy the condition?
输入格式
The first line of the input contains a single integer t (1≤t≤100) — the number of test cases. The desc
The first line of each test case contains the integer n (1≤n≤100).
Then one line follows, containing n integers a1≤a2≤…≤an (1≤ai≤107).
输出格式
输入样例 复制
3
5
1 2 3 4 5
1
1033
5
600 900 1300 2000 2550
输出样例 复制
10
0
4
数据范围与提示
In the first test case, we initially have a piece of size 1, so all final pieces must have size 1. The total number of steps is: 0+1+2+3+4=10.
In the second test case, we have just one piece, so we don't need to do anything, and the answer is 0 steps.
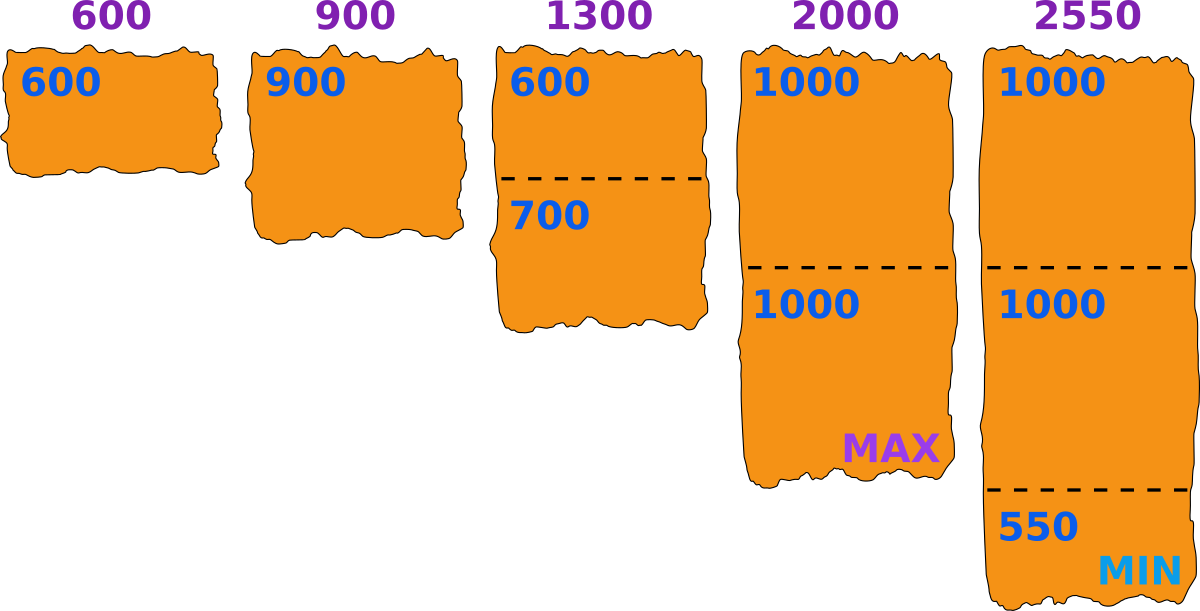
In the third test case, one of the possible cut options is: 600, 900, (600|700), (1000|1000), (1000|1000|550). You can see this option in the picture below. The maximum piece has size 1000, and it is less than 2 times bigger than the minimum piece of size 550. 4 steps are done. We can show that it is the minimum possible number of steps.