4021: 二叉排序树的基本操作
内存限制:32 MB
时间限制:1 S
标准输入输出
题目类型:传统
评测方式:文本比较
上传者:
提交:32
通过:18
题目描述
二叉排序树或者是一棵空树,或者是具有以下几条性质的二叉树:
1. 若它的左子树不空,则左子树上所有结点的值均小于它的根节点的值;
2. 若它的右子树不空,则右子树上所有结点的值均大于它的根节点的值;
3. 它的左右子树也分别为二叉排序树。
二叉排序树又可以被称为二叉查找树,根据上述定义的结构不难知道,它的查找过程十分简单,只需要通过不断的将当前结点的值与需要查找的值进行比较,如果相等则直接输出,如果要查找的值更小则深入至左子树进行比较,否则就深入右子树进行比较,直到找到相应的值或者进入了一棵不存在的子树为止。
其查找过程可以描述如下:

而其插入过程同样也十分简洁,可以描述如下:
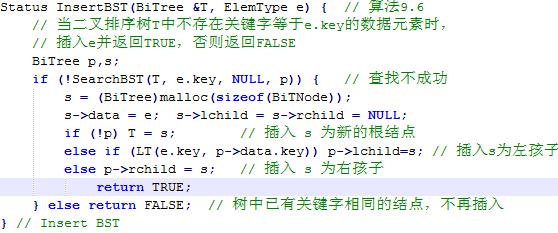
而删除操作可以描述为如下的两个算法:
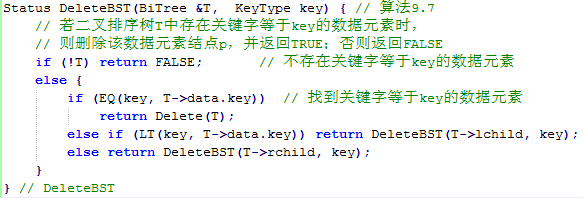

在本题中,读入一串整数,首先利用这些整数构造一棵二叉排序树。另外给定多次查询,利用构造出的二叉排序树,判断每一次查询是否成功。
输入格式
输入的第一行包含2个正整数n和k,分别表示共有n个整数和k次查询。其中n不超过500,k同样不超过500。
第二行包含n个用空格隔开的正整数,表示n个整数。
第三行包含k个用空格隔开的正整数,表示k次查询的目标。
输出格式
只有1行,包含k个整数,分别表示每一次的查询结果。如果在查询中找到了对应的整数,则输出1,否则输出0。
请在每个整数后输出一个空格,并请注意行尾输出换行。
输入样例 复制
8 3
1 3 5 7 8 9 10 15
9 2 5
输出样例 复制
1 0 1
数据范围与提示
在本题中,首先需要按照题目描述中的算法完成二叉排序树的构造过程,之后需要通过在二叉排序树中的不断向下查找,将需要查询的值与当前节点的值进行比较,直到确定被查询的值是否存在。
通过课本中的性能分析部分,不难发现二叉排序树的平均查找长度是和logn同数量级的,但是,在某些特殊情况下二叉排序树将会退化,使查找的效率大大降低,这时就需要引入二叉排序树的平衡操作,利用平衡二叉树来保证查找的效率始终维持在logn的数量级上。